 В честь начала спецкурса ( который, по-правде, начался две недели назад) "Анатомия сети" поделюсь парой сайтов, с которых, считаю адекватным начать этот курс. Оба сайта представляют собой карты. Карты Интернета. Но в довольно своеобразном смысле)
В честь начала спецкурса ( который, по-правде, начался две недели назад) "Анатомия сети" поделюсь парой сайтов, с которых, считаю адекватным начать этот курс. Оба сайта представляют собой карты. Карты Интернета. Но в довольно своеобразном смысле)1. Карта интернета.
Что есть интернет? Огромная сеть связанный гиперссылками страниц. Данные, запароленные и общедоступные, океан информации. Интернет, это 634 миллиона сайтов, 2.4 миллиарда пользователей в мире, по версии Pingdom (2012 г). Сложно себе представить столь огромные скопление единиц информации.
Но попробовать можно. В частности, существует такой проект, как The Internet Map. Проект создан с целью показать, как выглядит Интернет в целом на плоском графе. Правила формирования модели такие:За основу построения связи брались переходи пользователей между сайтами. Размер круга определяется посещаемостью сайта, цвет – национальной принадлежностью, а положение на карте – его связями с другими сайтами. Если два сайта имеют стабильный поток пользователей между ними, то они будут «стараться» расположиться ближе друг к другу.
На карте можно наблюдать скопления сайтов (кластеры) объединенные общими пользователями. На данный момент кластеризованно более чем 350 тысяч сайтов в соответствии с переходами пользователей между ними. Гиганты видны сразу же, однако, изучение картные будет довольно увлекательным занятием и для тех, кто умеет ориентироваться в интернете.
Особо выделяется три зоны (англо-американская, китайская и русская аудитории), однако разработчики уделили внимания и менее многочисленным кластерам:
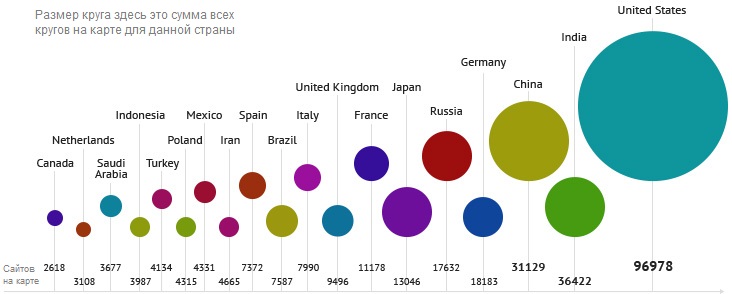
Однако, мало этого. Авторы сумели организовать этот каталог так, чтобы каждая вершина графа несла подробную информацию о сайте, а так же давала прямую ссылку и краткое описание его! Работа поистине заслуживающая высокой похвалы и изучения. Оставлю две ссылки на Habrahabr, если кого заинтересуют подробности составления такого каталога.
Однако, не стоит забывать, что отражённые на карте сайты - это вершина айсберга, это легко находимая, всем доступная, находящаяся в непрерывном внутреннем взаимодействии сеть. А что глубже? Всё чёрное пространство, так же заполнено сайтами, количество посещений и (или) связей которых с другими недостаточно, чтобы быть отражённым на карте. Это как со звёздами. По-правде в любой точке неба есть звезда. Просто многие из них слишком далеко удалены или слишком слабы, чтобы мы могли их разглядеть на небе. Иногда даже в телескоп. Это тёмное пространство называется Deep Web (Глубокая Сеть). Это множество сайтов, динамических страниц и прочих веб-ресурсов, не индексируемых поисковиками.

Привет! Здорово, не знал.
ОтветитьУдалитьПри взгляде на картинки выше, бросается в глаза ее качественная особенность:
Визуально можно разделить все сайты на 5 "звездных величин", 1-я: гиганты(Google, Yandex, vk, к стати, готов поспорить, что радиус кружка это логарифм числа пользователей), дальше, сравнивая с ними можно выделить вторую, сравнивая со второй - третью и т д до пятой. Что интересно, вокруг сайтов первой и второй величины образуется ярко выраженный поясок сайтов 4-5 величины. Для третьей это тоже заметно, дальше- практически нет.
Если близость кружков связана с потоком пользователей между ними, то я бы ожидал, что вокруг первой будет пояс из второй-третьей а мелочь расположится между ними. Но почему, на самом деле, к самым большим липнут самые маленькие?
Есть подозрение, что это просто артефакт алгоритма построения картинки. Если бы самых больших не было, мелочь расположилась бы равномерно, но самые большие просто раздвигают ее, так как там введено что-то типа сил взаимодействия между кружками и взаимной посещаемости пропорциональна сила притяжения между двумя сайтами, а сила отталкивания у всех одинаковая и (наверное) растет с уменьшением расстояния. По крайней мере я взялся бы строить подобную картинку именно так. Короче не факт, что все закономерности, которые можно тут увидеть отражают "природу вещей".
Да, согласна, с расстоянием всё не так просто как я написалал. Думаю, тут задействован принцип "оптимального расположения". Т.е. чтобы все находились максимально равноудалённо от связанных объектов, а гиганты имели минимальное расстояние, ближе которого они стоять не должны. Ну, мне так кажется.
УдалитьВот тут есть про алгоритм построения (видео) : http://the-internet-map.blogspot.ru/2012/09/map-layout-process-video.html
УдалитьПосмотрел видео, и до меня примерно дошло как оно работает. Извини,что засоряю твой блог. Просто мне очень понравилась их работа, а написать у себя я никогда не соберусь^^" ...
УдалитьРебята написали некоторую функцию "энергии" системы. В ней каждой паре сайтов {i,j} соотв. слагаемое наподобие:
K[i,j]*L^2[i,j]-a/L[i,j],
где L[i,j]- расстояние между кружками обозн. сайты, K[i,j]- коэффициент пропорциональный взаимной посещаемости, a- одинаковая для всех положит. константа. Первый член соотв. "резиночке" связывающей два сайта. чем больше взаимная посещаемость, тем она туже. Второй- взаимное Кулоновское отталкивание, чтобы все не стянулось в одну точку. Они конечно могли взять немного другую формулу, но думаю идея такая.
Чтобы нарисовать картинку, надо найти расположение кружков, реализующее глобальный минимум этой функции. Это дико вычислительно тяжелая задача, так как у такой функции будет очень сложный рельеф с кучей локальных минимумов. Они решают ее методом simulated annealing (симулированный отжиг, отжиг-термин из металлургии). Сначала кружки располагаются случайно. На каждом шаге кружок перепрыгивает в ту сторону, в которую его тянет равнодействующая упругих и Кулоновских сил, плюс случайная добавка, тем большая, чем выше "температура"(Т) системы. Если Т=0, то скорее всего, система сделает несколько шагов и застрянет в *локальном* минимуме, который будет довольно далек от глобального. Если взять высокую температуру, то система не устаканится никогда. По этому, сначала берут высокую температуру и постепенно ее понижают. Эмпирически известно (понятия не имею, есть ли этому строгое доказательство), что если понижать температуру достаточно медленно, то к моменту когда будет достигнута Т=0, система окажется довольно близко от глобального минимума. Это похоже на процедуру отжига куска металла, когда его разогревают до бела и медленно и равномерно остужают, в результате получается наиболее прочная кристаллическая структура по всему объему и без внутр. напряжений.
Вот такое вот забавное применение вычислительной физики..
О, реально круто!) Спасибо за очень полезное дополнение)
УдалитьОй.. перед буквой а должен стоять плюс. это я по привычке написал притягивающий Кулон вместо отталкивающего. и K[i,j]>0, есст-но.
Удалить