Бутылка Клейна

Сегодняшний пост будет посвящён бутылке Клейна. Этот объект тесно связан с листом Мёбиуса, о котором уже говорилось ранее, и с названием этого блога :) 

Построение

В сущности же, бутылка Клейна очень простая вещь( опять же, если определять её нативно). 

1 способ 

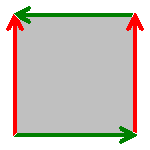Рис. 1 Развёртка бутылки Клейна

Возьмём квадрат и покрасим его противоположные стороны так, как показано на рисунке 1, задав при этом направление прохождения этих сторон. Теперь склеим противоположные стороны так как показано на рисунке, чтобы цвет и направления стрелок при склейке совпадали. Сначала красные, потом зелёные. После отождествления красных точек получим цилиндр. С зелёными будет похитрее, учитывая что направление должно совпадать. 

Замечание: попытайтесь представить это себе, прежде чем изучать рисунок ниже.

Кликните на картинке чтобы увидеть анимацию

Фиолетовым отмечена полоса, которая в конце станет листом Мёбиуса, а изначальная поверхность окрашена в белый цвет снаружи и в зелёный внутри.

2 способ 

Отмечу сразу, что результат второго способа ничем не отличается от первого. Разница только в том, как легче представлять процесс и результат.  


Склеим теперь сначала зелёные края. Получим уже известную ленту Мёбиуса. А теперь красные. Края ленты склеятся в трубочку. Получится поверхность без края (это свойство, впрочем,  не является характерным. Например сфера, куб, тетраэдр и другие правильные многогранники края не имеют, а имеют только поверхность). 

Однако есть одно но, которое сильно влияет на свойства бутылки Клейна. Полученный объект не должен иметь самопересечений. Если вы попробуете проделать описанные преобразования вручную, то чтобы всё склеить правильно придётся сделать прорезь ( как это видно на всех приведённых объектах). Однако в самой бутылке Клейна такой прорези быть не должно. Её и нет в четырёхмерном пространстве ( \(\mathbb{R}^4 \) ), куда, в сущности, и вкладывается бутылка Клейна. В \(\mathbb{R}^3 \) без самопересечений она быть помещена не может. Поэтому все примеры и реализации бутылки в реальной жизни - это лишь её проекции в наше трёхмерное пространство. Как это понять? Вспомните лист Мёбиуса. По-сути же это кусок плоскости, т.е. двухмерный объект, просто определённым образом склеенный. Кольцо, например, спокойно проецируется на плоскость. Однако после склейки листа Мёбиуса уже невозможно уложить в плоскость ( \(\mathbb{R}^2 \) ) и без самопересечений он существует только в \(\mathbb{R}^3 \) . 

Замечание: попробуйте :) допускаются любые растяжения и сжатия. всё кроме добавления или удаления уже существующих дырок.  

То же происходит и с бутылкой Клейна. Она есть трёхмерный объект, который в  \(\mathbb{R}^3 \) быть вложен не может. Поэтому всё что мы видим - лишь проекция настоящей бутылки Клейна. 

История названия

Исходное название бутылки Клейна - "Klein Fla-e-che" (Fläche = поверхность) поверхность Клейна. Но слово Fläche было искажено в процессе популяризации и стало читаться как  Fla-s-che (бутылка) из-за преобладания английского языка и прочно утвердилось в математической науке. Позднее термин "бутылка Клейна" также стал использоваться и в Германии.

Применение

Честно говоря, я поняnия не имею какое применение может быть у бутылки Клейна :) То, что я видел или читал, скорее стилизация подо что-то или просто мифические идеи. Например говорят что алхимики очень алкали такой сосуд, у которого не было бы внутренности и внешности ( бутылка Клейна как раз обладает таким свойством).

• Игра: "Топус"

• Открывашки бутылок:

•   Скульптуры:

 

• Cумки (даже шапки бывают ^^""""):

• Чашки ну и конечно чайники (:

Замечание: как видите, чайник этот не вполне бутылка Клейна, но не сложно довести его до нужного состояния) Так и у нас тут — я вряд ли смогу абсолютно всё рассказать, но я постараюсь сделать так, чтобы при должном интересе это было не сложно исследовать самим :)

Кстати говоря, процесс выдувания таких стеклянных бутылок - крайне трудоёмкий и только стеклодувы высокого класса могут это сделать (потому что нужно оставлять дырочку в поверхности. Понятно, что живи мы в \(\mathbb{R}^4 \) никаких бы проблем не было ) 

Алгебраический подход. Определение, формулы построения

Определение

Бутылка Клейна — это неориентируемая поверхность, определённая правилами склейки указанными выше (то есть двумерное многообразие).
Замечу, что изгибать бутылку можно как угодно. От этого она, как и лист Мёбиуса, своих характерных свойств не потеряет. Поэтому она, в принципе, совершенно не обязана выглядеть как бутылка. Например рисунок справа тоже представляет собой бутылку Клейна ( такою форму называют восьмёрка) и задаётся она системой параметрических уравнений : 

\(  \begin{cases} x(r, \alpha, \beta) = &  \left( r + \cos{\frac{\alpha}{2}} \sin{\beta} - \sin{\frac{\alpha}{2}} \sin{2 \beta}\right) \cos{\alpha} \\ y(r, \alpha, \beta) = &  \left( r + \cos{\frac{\alpha}{2}} \sin{\beta} - \sin{\frac{\alpha}{2}} \sin{2 \beta}\right) \sin{\alpha}\\  z(r, \alpha, \beta) = & \sin{\frac{\alpha}{2}}\sin{\beta}+ \sin{ \frac{\alpha}{2}}\sin{2\beta} \end{cases} \)

 где  \( 0 \le \alpha < 2\pi \) ,  \( 0 \le \beta < 2\pi \) и \(0 \le r \le 1\) - сферические координаты

Или неявным уравнением вида \( (x^2+y^2+z^2+2y-1)({(x^2+y^2-2y-1)}^2 - 8z^2)+16xz(x^2+y^2+z^2-2y-1)=0\). 

В этой вкладке слева ссылки на аплеты по теме бутылки Клейна.

Опять же, можете построить его в WolframAlpha, но на этот раз достаточно просто набить в поисковике "klein bottle"

Замечание: я не собираюсь приводить здесь систему уравнений задающую бутылку Клейна такой, какой мы её привыкли видеть ввиду её громоздкости.

А ещё там же вы можете найти много приложений, в которых можно повертеть и помучить :)

Иллюстрация разрезания.

Ещё один способ раскромсать бутылку на что-нибудь любопытное:

Кликните на картинке, чтобы увидеть анимацию

Здесь бутылка Клейна разрезается на два зеркальных друг другу листа Мёбиуса (т.е. один перекручен направо, а  другой налево. Как вы думаете, переводится ли один в другой? ) Между листами вклеена обычная лента ( кольцо), внешняя часть которого покрашена в белый, а внутренняя в голубой.  Вообще можно разрезать бутылку Клейна так, чтобы получить один лист Мёбиуса, но об этом вы уже знаете (нужно просто резать так же как склеивали во втором случае)

Заключение

В сущности, бутылка Клейна кажется не очень-то серьёзным объектом. Ну склеили края ленты, ну молодцы, пользы-то никакой. По-правде от всего есть польза. В частности, склеивая одностороннюю ленту Мёбиуса мы всё ещё получаем одностороннюю неориентируемую поверхность. А что будет если и ещё склеить? это уже нашему понимаю не поддаётся, потому как представлять это нужно в четырёхмерном пространстве. А что если склеивать не противоположные точки края ленты Мёбиуса, а накрест лежащие?
И наконец, что будет если склеивать не ленту Мёбиуса и не кольцо а, скажем, обыкновенный круг? 

Замечание: подумайте над ответом на этот вопрос в двух случаях: 

1. все точки края склеим в одну. Получим сферу
2. диаметрально противоположные точки края склеиваются между собой. 

Так вот в последнем случае получается проективное пространство. А это уже — целая тема для будущих постов)

Ссылки

1. Imaging maths - Inside the Klein bottle — замечательная статья в которой можно посмотреть кучу анимации по теме и может даже почитать (eng)
2. Анимационный фильм о Бутылке Клейна, созданный в 2010 г. при Свободном Университете г. Берлин (Freie Universität Berlin), включает изображение поездки по Бутылке и изначальное описание Феликса Клейна.
3. Статья, стиль которой мне понравился.